2. Regression with multiple input variables

Multiple Features

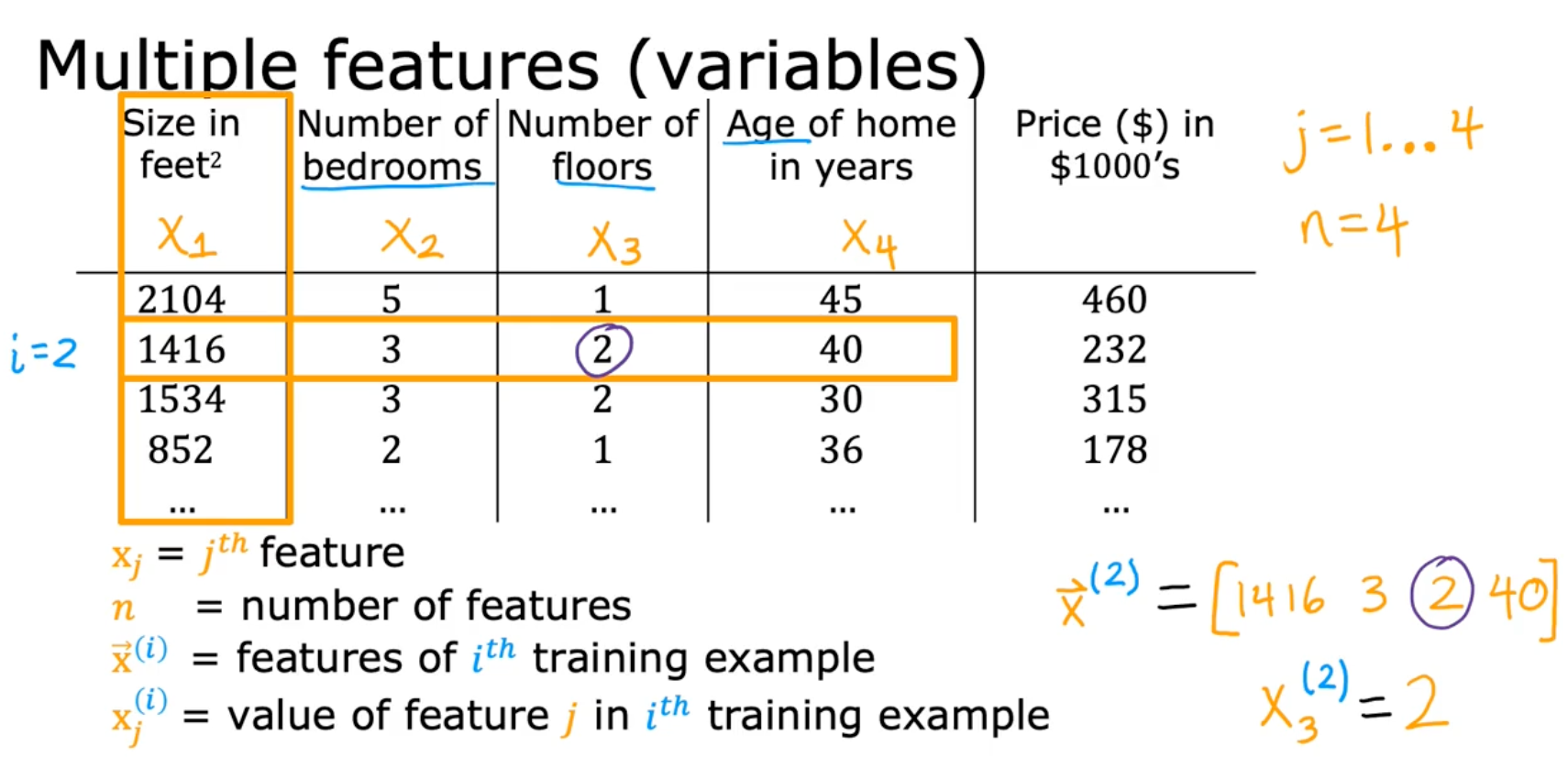
Model

$$f_w,_b(x) = w_1x_1+w_2x_2+...+w_nx_n+b$$

• parameters of the model

$\overrightarrow{w}$ = [w1 w2 w3 .. wn]

• number

b

• vector

$\overrightarrow{x}$ = [x1 x2 x3 .. xn]

Simplified - multiple linear regression

$f_w,_b(x) = w_1x_1+w_2x_2+...+w_nx_n+b = \overrightarrow{w}\cdot\overrightarrow{x}+b$

Vectorization

Parameters and features

$\overrightarrow{w}$ = [w1 w2 w3] (n = 3)

b is a number

$\overrightarrow{x}$ = [x1 x2 x3 .. xn]

w = np.array([1, 2, 3])
b = 4
x = np.array([10, 20, 30])

Without vectorization

$f_{\overrightarrow{w}},_b(\overrightarrow{x}) = w_1x_1+w_2x_2+...+w_nx_n+b$

f = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + b

$= f_{\overrightarrow{w}},_b(\overrightarrow{x}) = \sum_{j=1}^{n}w_jx_j+b$

f = 0
for j in range(n):
	f = f + w[j] * x[j]
f = f + b

With vectorization

$f_{\overrightarrow{w}},_b(\overrightarrow{x}) = \overrightarrow{w}\cdot\overrightarrow{x}+b$

f = np.dot(w,x) + b

vectorization calculate each columns in parallel

• much less time
• efficient → scale to large dataset

Gradient descent

$\overrightarrow{w}$ = (w1 w2 … w16)

$\overrightarrow{d}$ = (d1 d2 … d16)

w = np.array([0.5, 1.3, ... , 3.4])
d = np.array([0.3, 0.2, ... , 0.4])

Compute $w_j = w_j - 0.1 d_j$ for $j = 1 ... 16$

Without vectorization

w1 = w1 - 0.1d1

…

w16 = w16 - 0.1d16

for j in range(16):
	w[j] = w[j] - 0.1 * d[j]

With vectorization

$\overrightarrow{w}=\overrightarrow{w}-0.1\overrightarrow{d}$

w = w - 0.1 * d

Gradient descent for multiple regression

Previous notation

Parameters

$w_1,...,w_n$

$b$

Model

$f_{\overrightarrow{w},b}(\overrightarrow{x})=w_1x_1+...+w_nx_n+b$

Cost function

$J(w_1,...,w_n,b)$

Gradient descent

repeat {

$w_j=w_j-a\frac{d}{dw_j}J(w_1,...w_n,b)$

$b=b-a\frac{d}{dw_b}J(w_1,...w_n,b)$

}

Vector notation

Parameters

$\overrightarrow{w}=[w_1...w_n]$

$b$

Model

$f_{\overrightarrow{w},b}(\overrightarrow{x})=\overrightarrow{w}\cdot\overrightarrow{x}+b$

Cost function

$J(\overrightarrow{w},b)$

Gradient descent

repeat {

$w_j = w_j - a\frac{d}{dw_j}J(\overrightarrow{w},b)$

$b = b - a\frac{d}{dw_b}J(\overrightarrow{w},b)$

}

Gradient Descent

One feature

repeat {

$w = w - a \frac{1}{m}\sum_{i=1}^{m}(f_w,_b(x^{(i)})-y^{(i)})x^{(i)}$

• $\frac{1}{m}\sum_{i=1}^{m}(f_w,_b(x^{(i)})-y^{(i)})x^{(i)} = \frac{d}{dw}J(w,b)$

$b = b - a\frac{1}{m}\sum_{i=1}^{m}(f_w,_b(x^{(i)})-y^{(i)})$

simultaneously update w, b

}

n features (n ≥ 2)

repeat {

j = 1 : $w_1 = w_1 - a \frac{1}{m}\sum_{i=1}^{m}(f_{\overrightarrow{w},b}(\overrightarrow{x}^{(i)})-y^{(i)})x^{(i)}$

• $\frac{1}{m}\sum_{i=1}^{m}(f_{\overrightarrow{w}},_b(\overrightarrow{x}^{(i)})-y^{(i)})x^{(i)} = \frac{d}{dw_1}J(\overrightarrow{w},b)$

$b = b - a\frac{1}{m}\sum_{i=1}^{m}(f_{\overrightarrow{w},b}(\overrightarrow{x}^{(i)})-y^{(i)})$

simulatenously update $w_j$ (for $j = 1,..,n)$ and $b$

}

An alternative to gradient descent

Normal equation

• only for linear regression
• solve for w, b without iterations
• need to know
  • Normal equation method may be used in machine learning libraries that implement linear regression
  • Gradient descent is the recommended method for finding parameters w, b
• disadvantages
  • doesn’t generalize to other learning algorithms
  • slow when number of features is large (> 10,000)

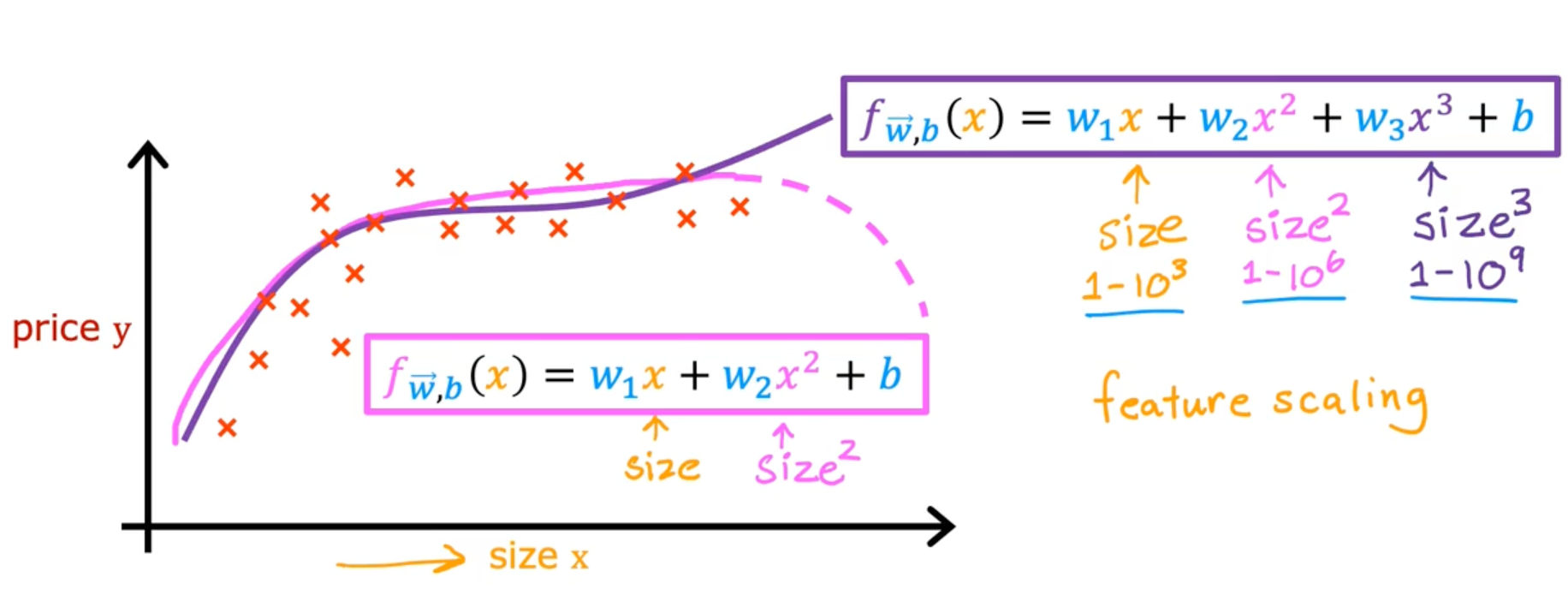
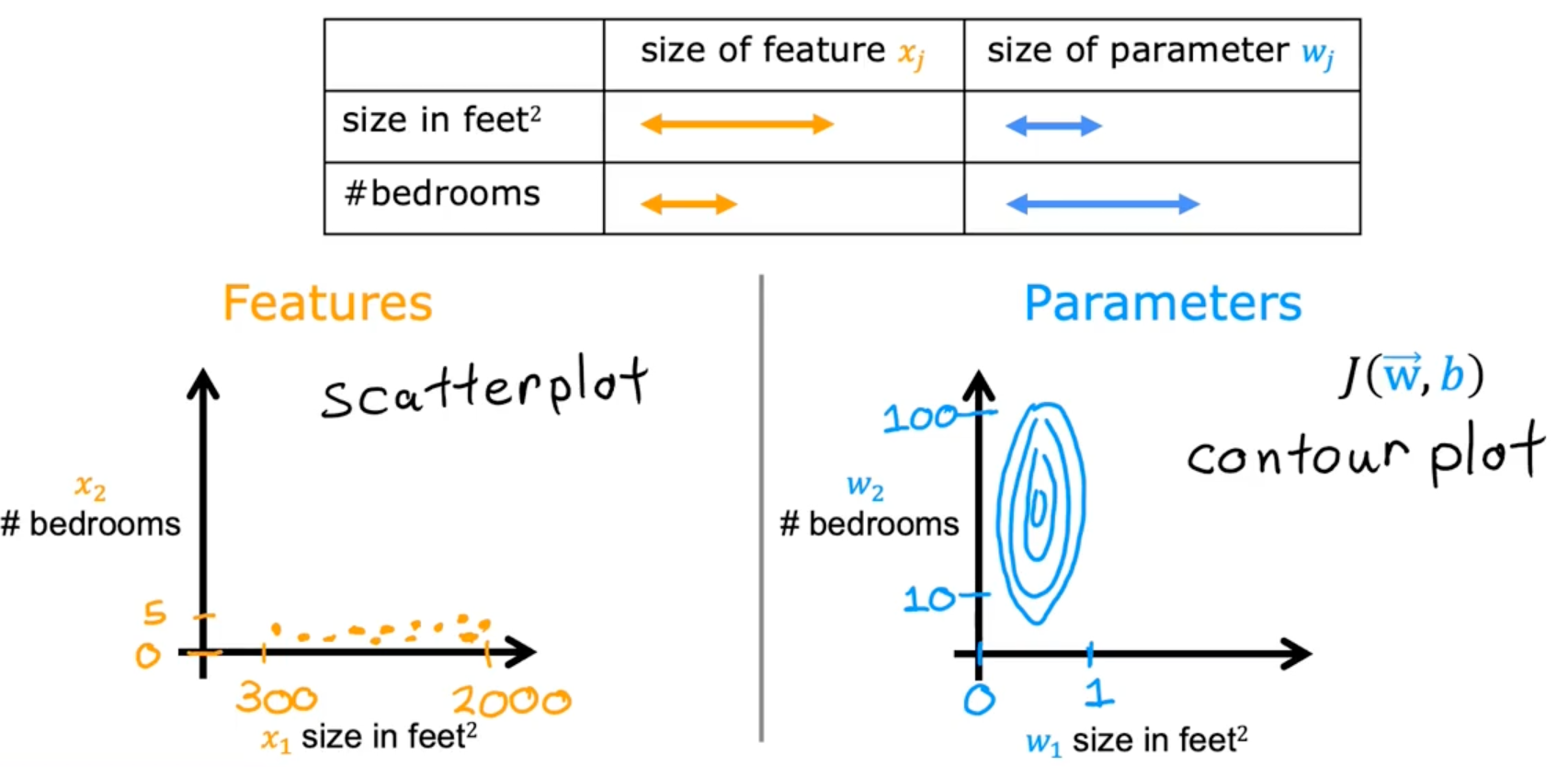
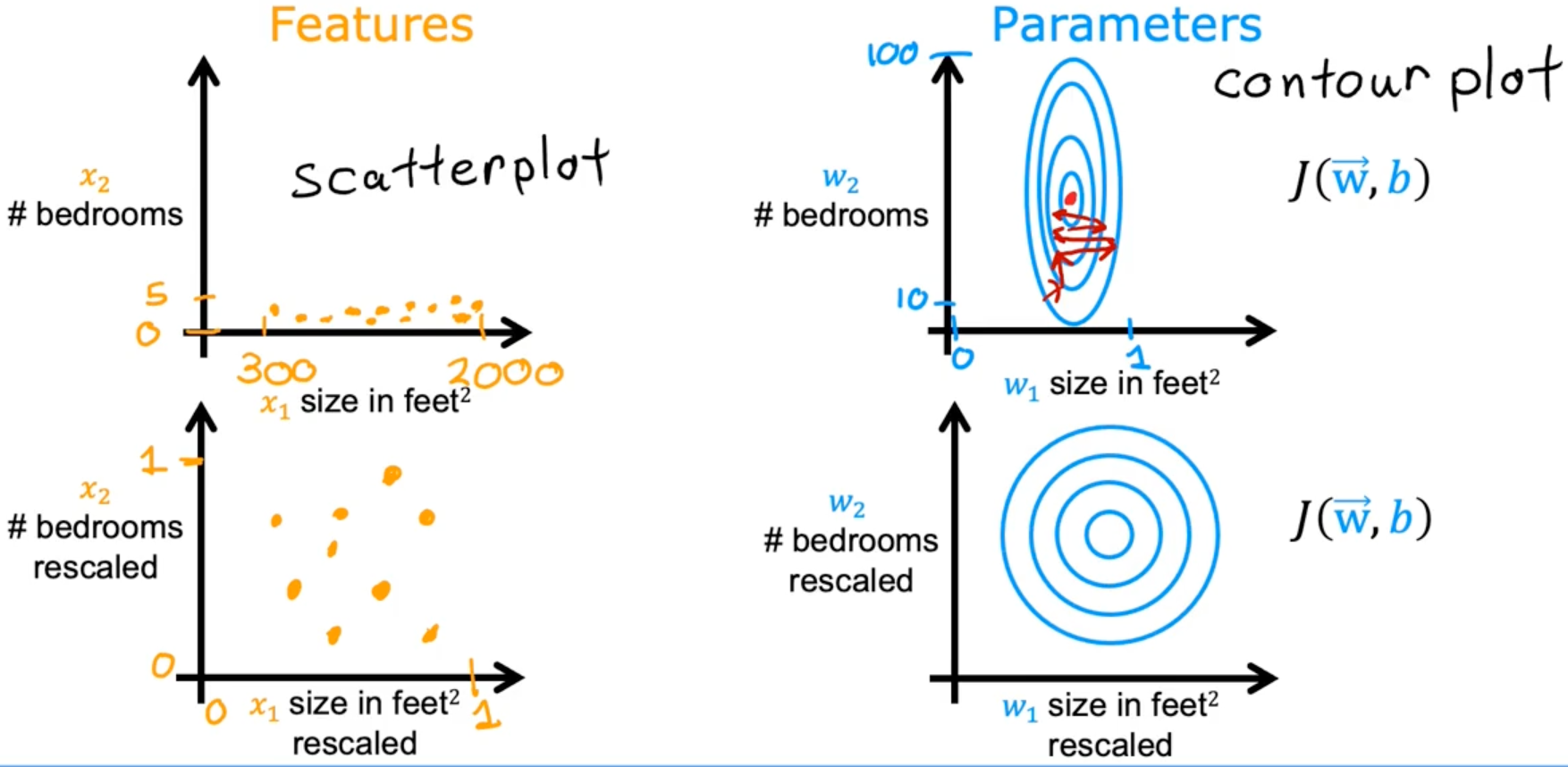
Feature scaling

Feature scaling enables gradient descent to run much faster by rescaling the range of each features

• aim for about -1 ≤ $x_j$ ≤ 1 for each feature $x_j$

  • acceptable ranges
    • -3 ≤ x ≤ 3
    • -0.3 ≤ x ≤ 0.3
  • Okay, no rescaling
    • 0 ≤ x ≤ 3
    • -2 ≤ x ≤ 0.5
  • rescaling
    • -100 ≤ x ≤ 100
    • -0.001 ≤ x ≤ 0.001
    • 98.6 ≤ x ≤ 105

• example

  

  

  

Mean normalization

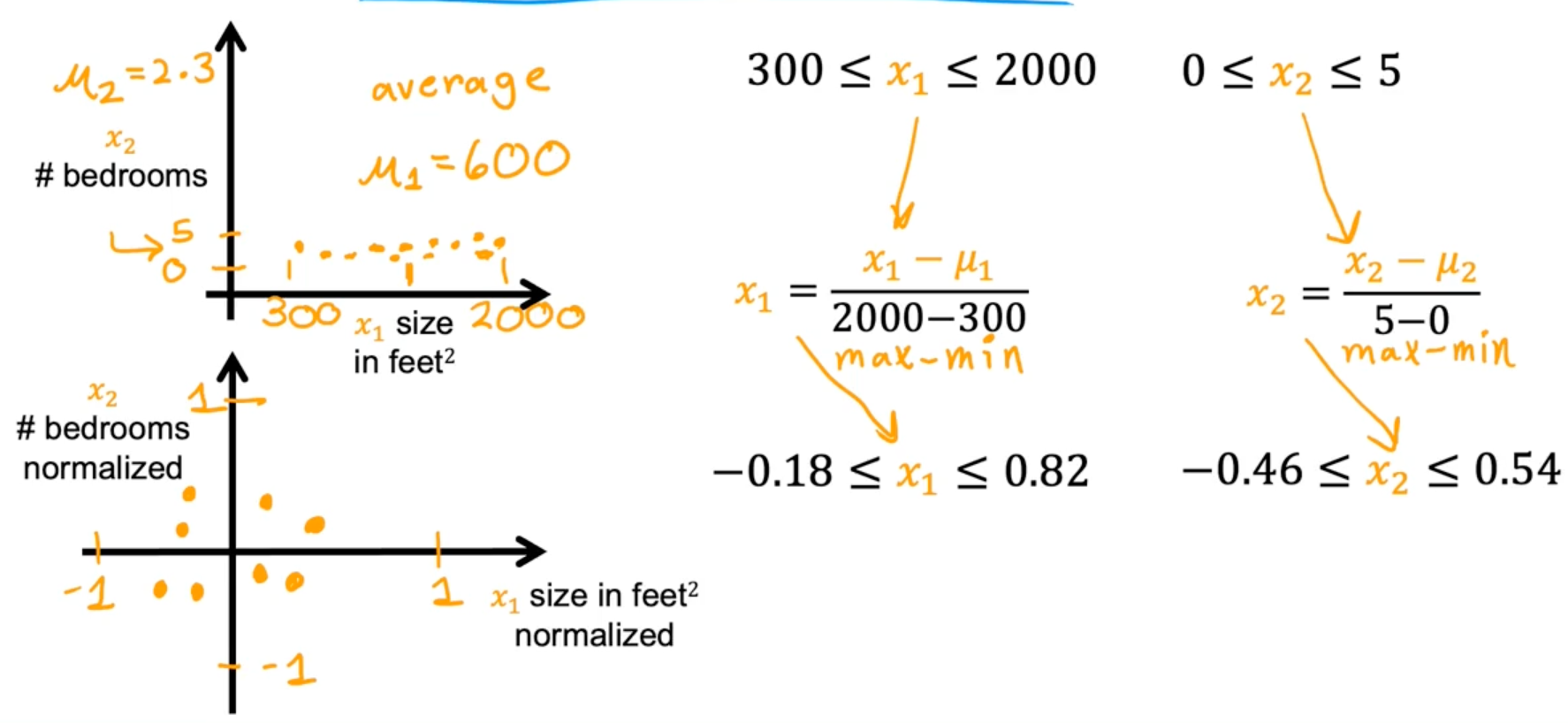
Z-score normalization

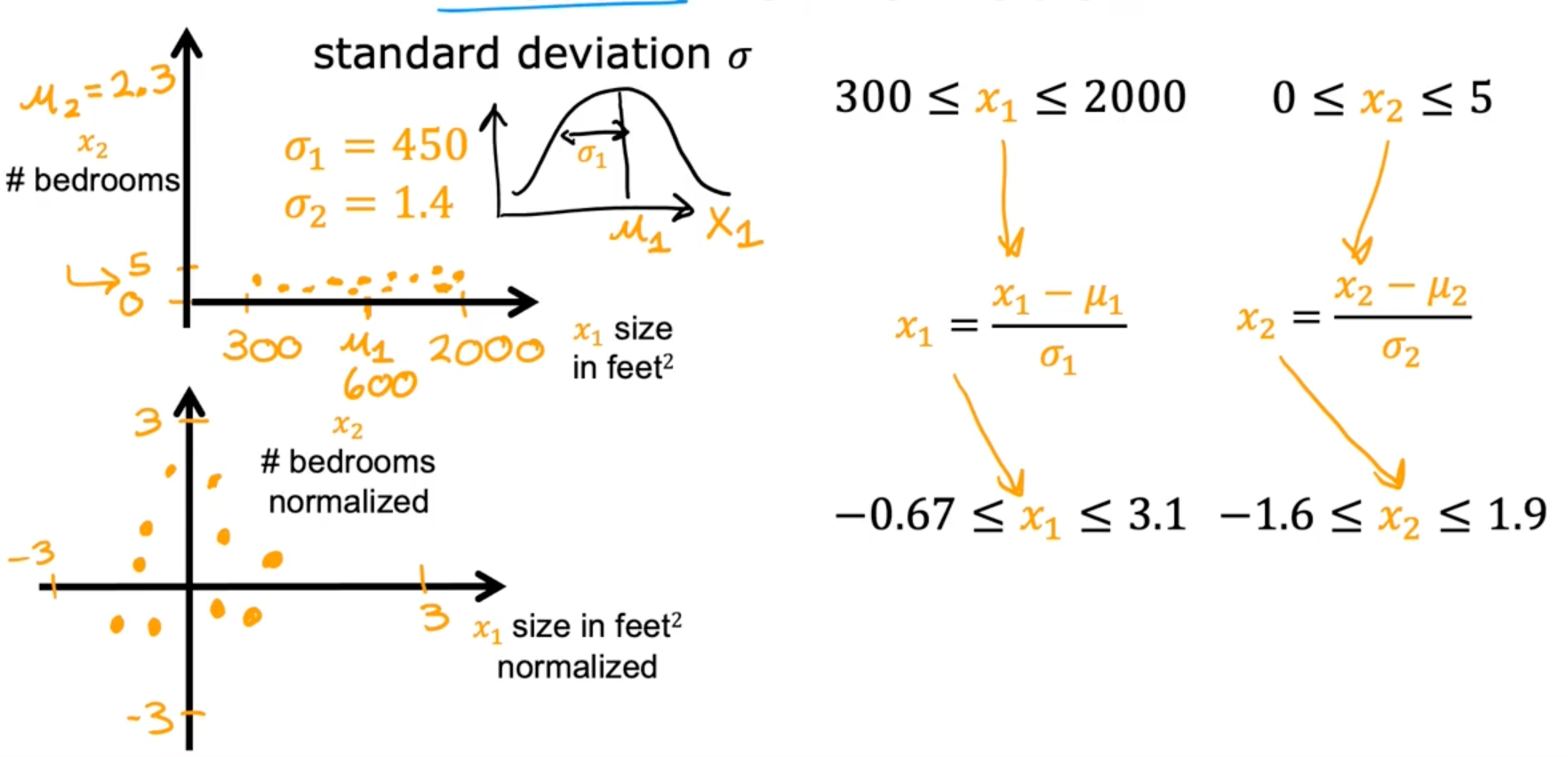
Checking Gradient descent for convergence

Choosing the learning rate

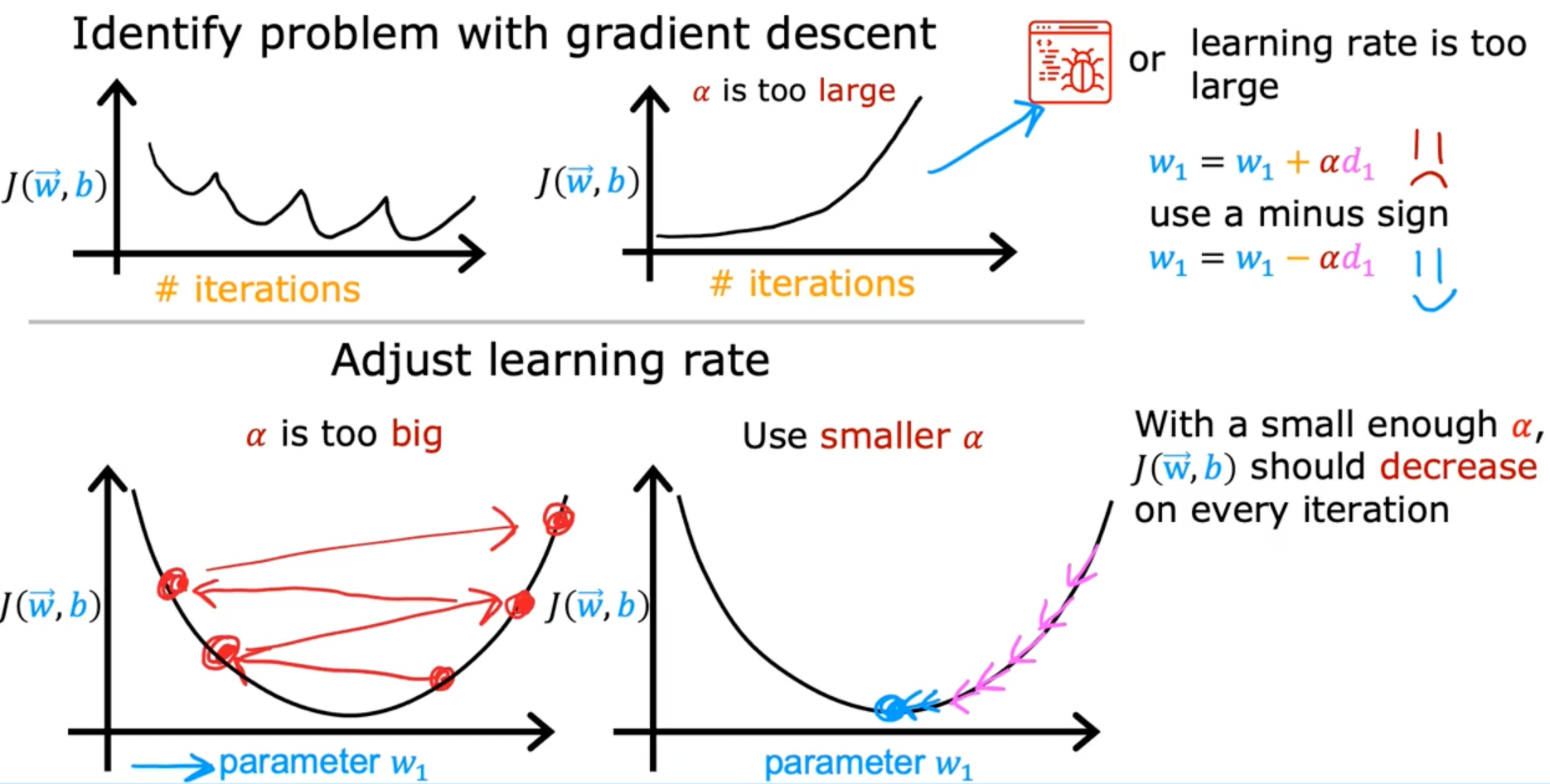
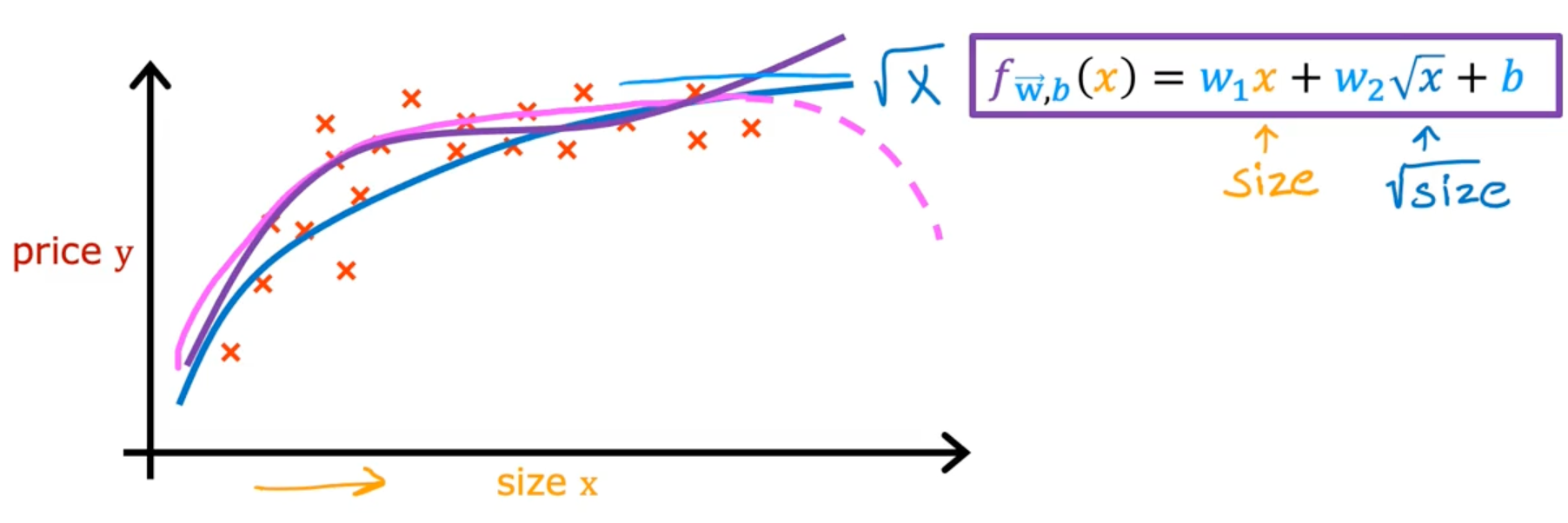
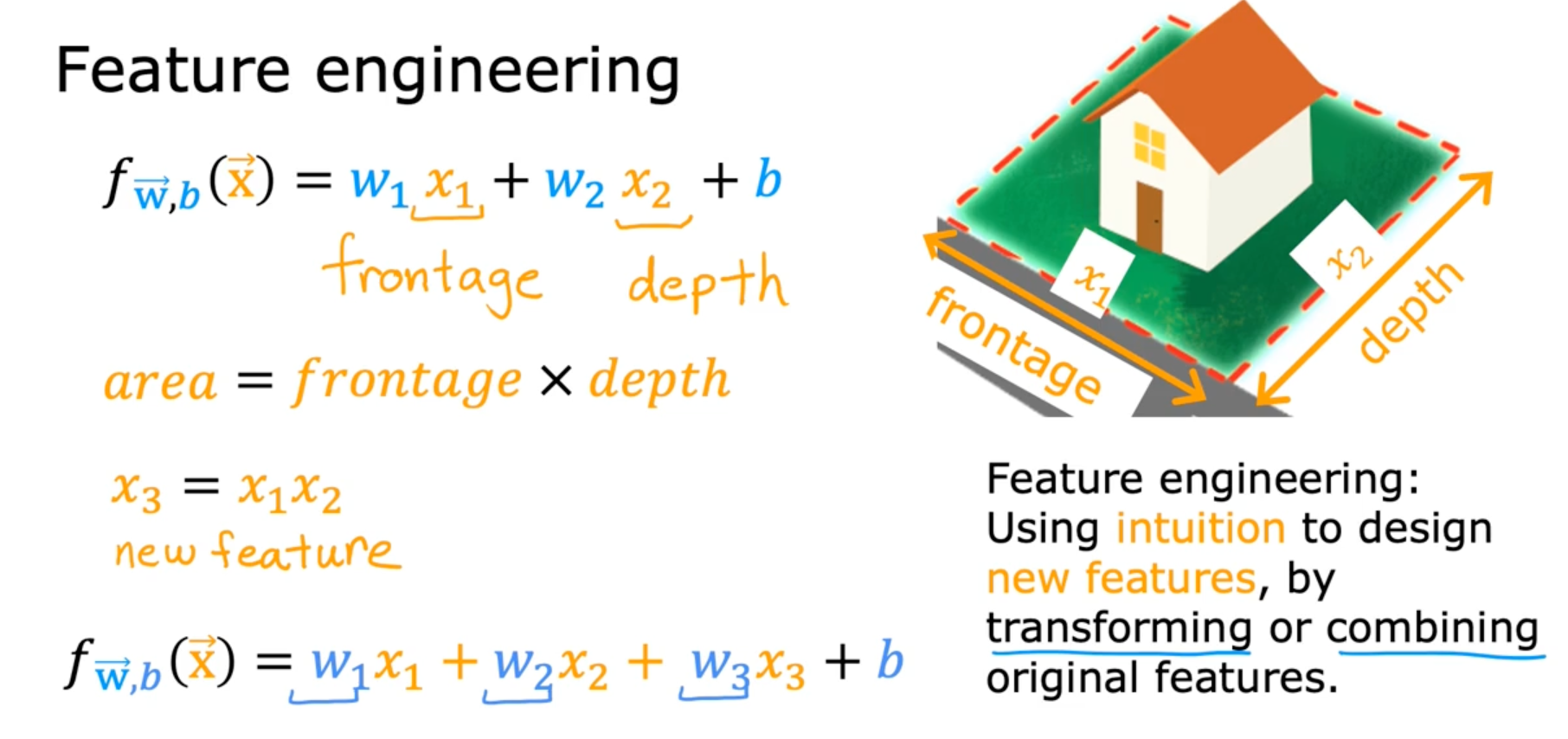
Feature engineering

Polynomial regression