Clustering

What is clustering?

• clustering algorithm looks at a number of data points and automatically finds data points that are related or similar to each other
• In supervised learning, the dataset included both the inputs x as well as the target outputs y
• In unsupervised learning, you are given a dataset with just x, but not the labels or the target labels y

Applications of clustering

• Grouping similar news
• Market segmentation
• DNA analysis
• Astronomical data analysis

K-means intuition

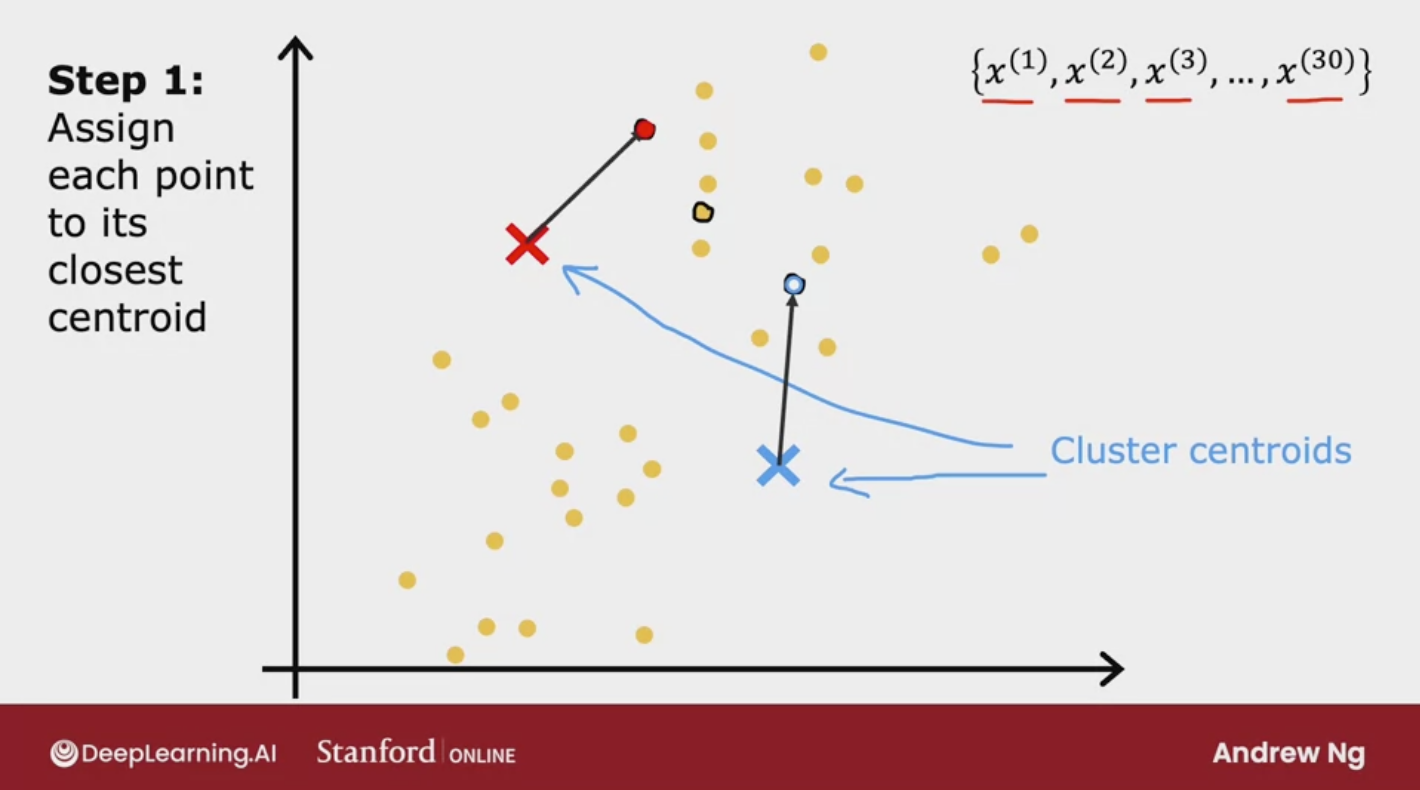
• Take a random guess at where might be the center of the clusters
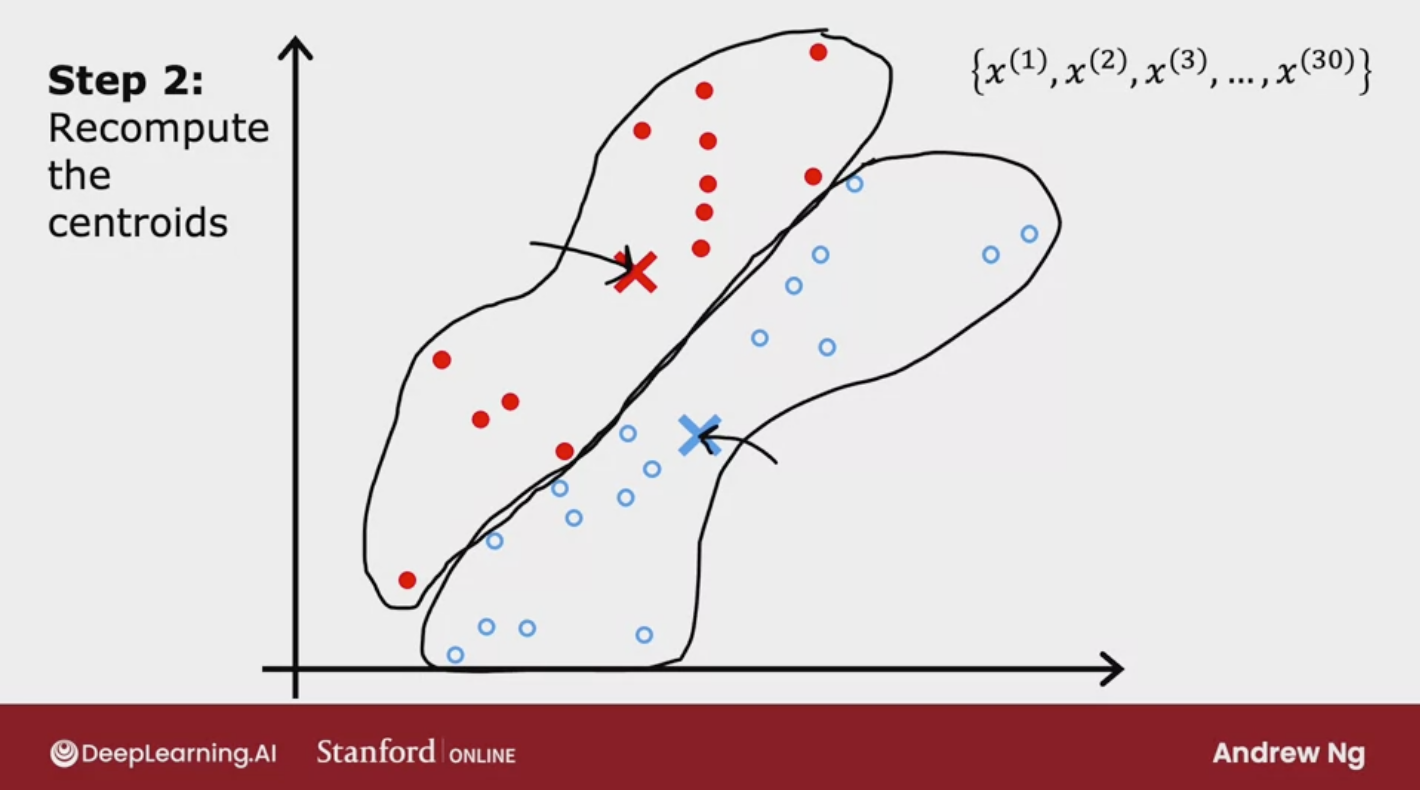
  • The first is assign points to cluster centroid and the second is move cluster centroids
  • Repeat until it finds that there are no more changes to the points or to the locations of the clusters centroids

K-means algorithm

• $\mu$ are the vectors that have the same dimensions
• Corner cases
  • when a cluster has 0 points assigned to it
    • delete the cluster or initialize one more random cluster

Optimization objective

• $c^{(i)}$ = index of cluster (1,2,…,K) to which example $x^{(i)}$ is currently assigned
• ${\mu }_k$ = cluster centroid k
• ${\mu }_{c^{(i)}}$ = cluster centroid of cluster to which example $x^{(i)}$ has been assigned

Cost function

• Distortion function

$$J(c^{(i)},...,c^{(m)},{\mu }_1,...,{\mu }_k)=\frac{1}{m}\sum _{i=1}^m||x^{(i)}-{\mu }_{c^{(i)}}|{|}^2$$ $$mi{n}_{c^{(i)},...,c^{(m)},{\mu }_1,...,{\mu }_k}J(c^{(i)},...,c^{(m)},{\mu }_1,...,{\mu }_k)$$

Initializing K-means

• Choose $K<m$
• Randomly pick $K$ training examples
• Set ${\mu }_1$,${\mu }_2$,…,${\mu }_k$ equal to these $K$ examples

Random initialization

For i = 1 to 100 {
  # Randomly initialize K-means
  # Run K-menas. Get c_1,...c_m, mu_1,...mu_k
  # Compute cost function (distortion)
}
# pick set of clusters that gave lowest cost J

Choosing the number of clusters

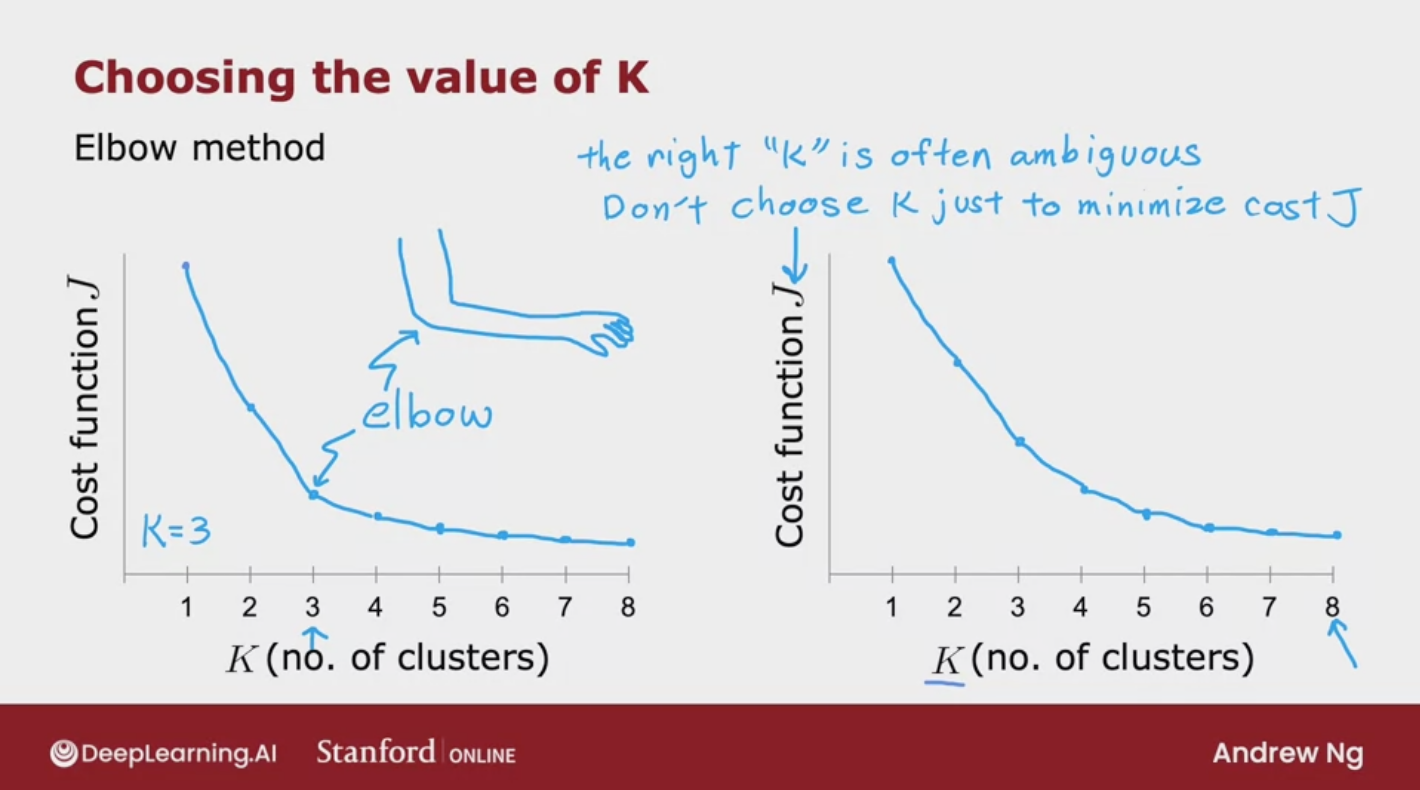
• Elbow method
  • Minimizing the number of cluster is not a good practice
  • Evaluate K-means based on how well it performs on that later purpose