Reducing the number of features
- Commonly used by data scientists to visualize the data, to figure out what might be going on
Examples
Car measurements
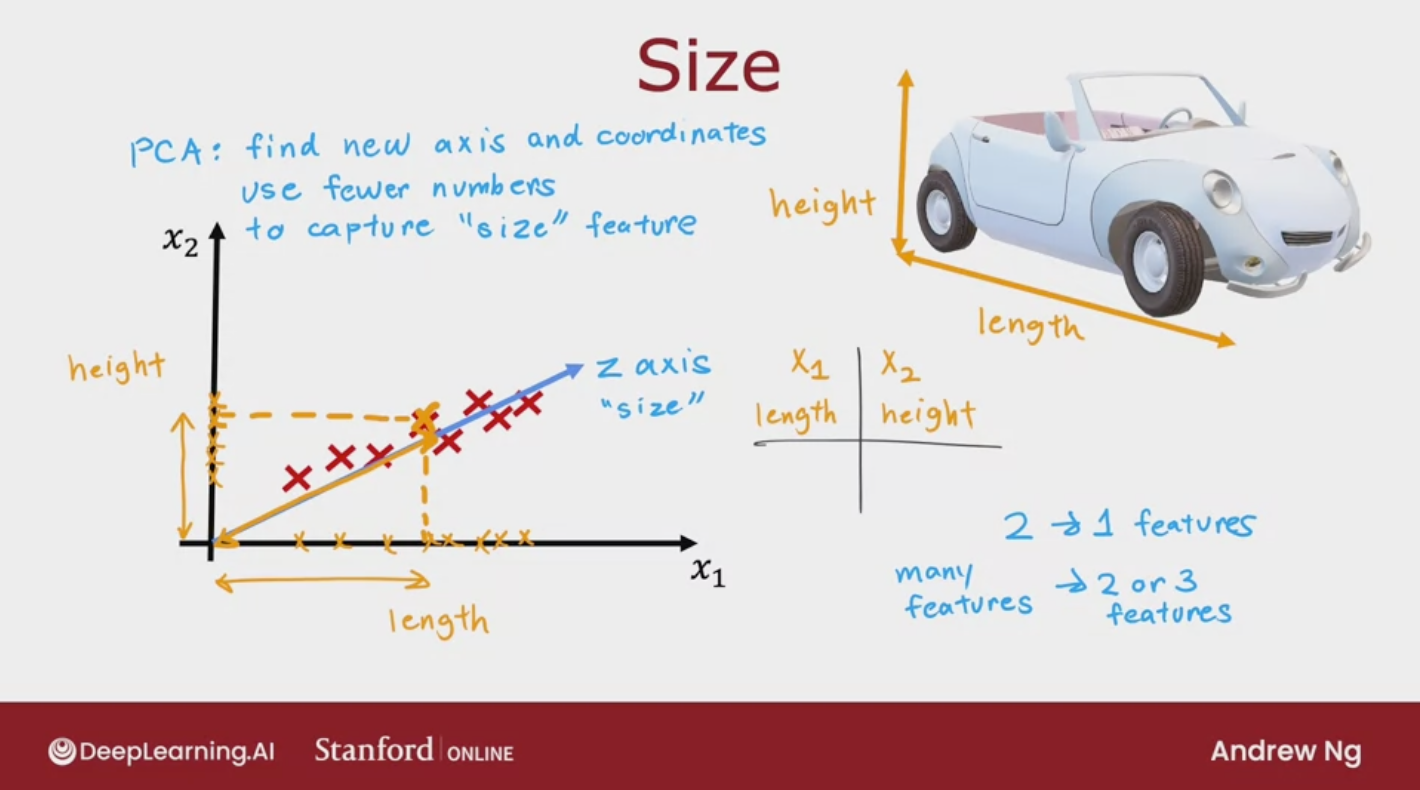
From 3D to 2D

Data visualization

PCA algorithm
- replaces two features with one feature

- Choose the least different axis

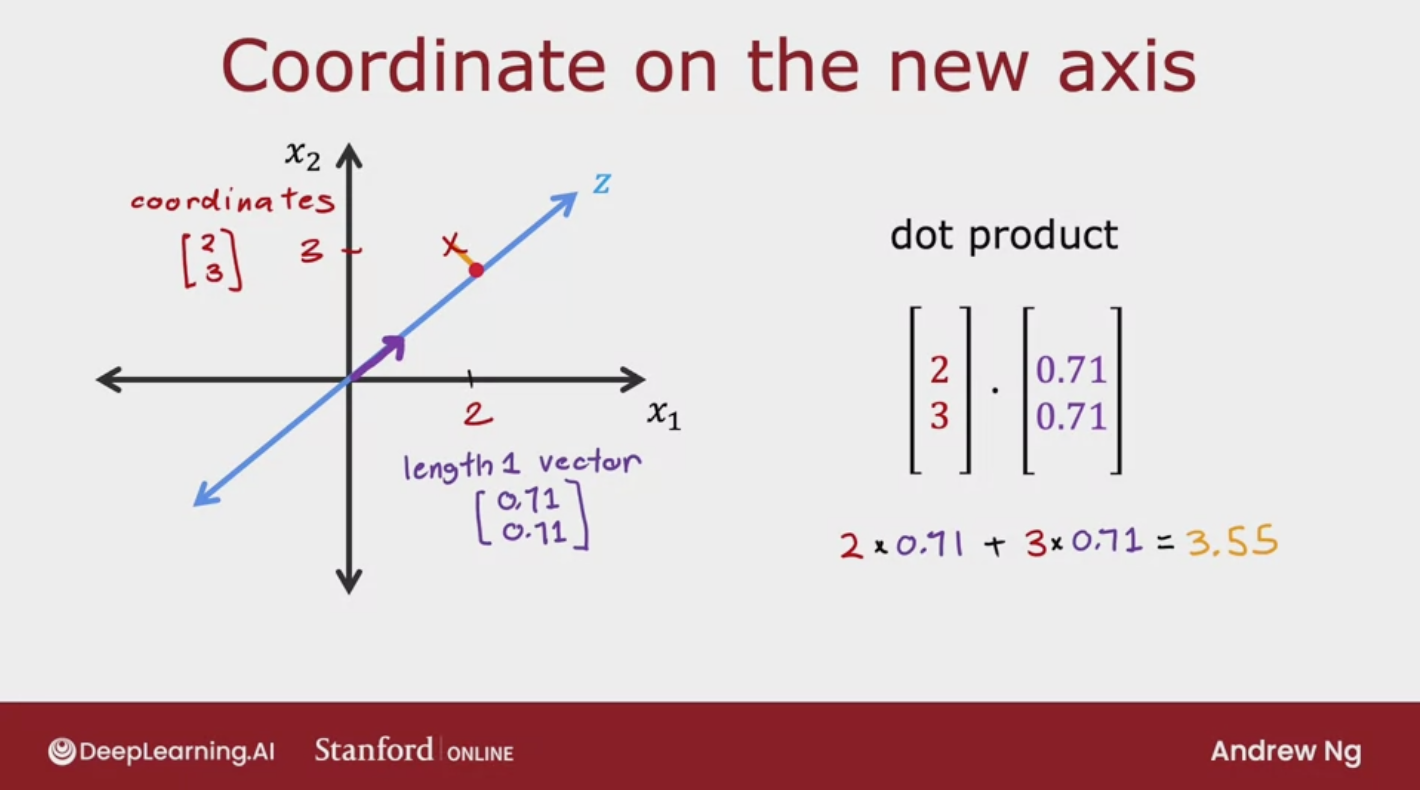
- Coordinate on the new axis: dot product
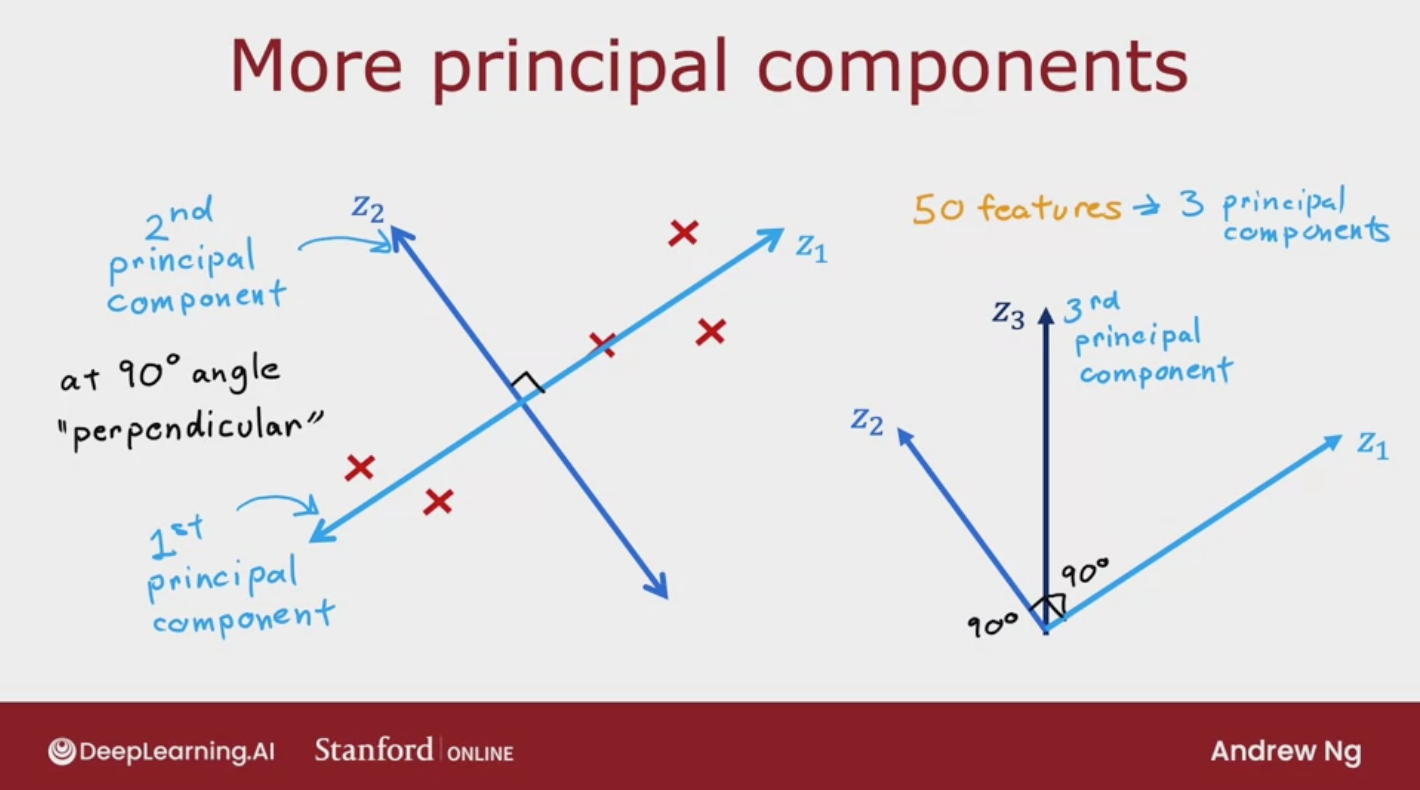
More principal components
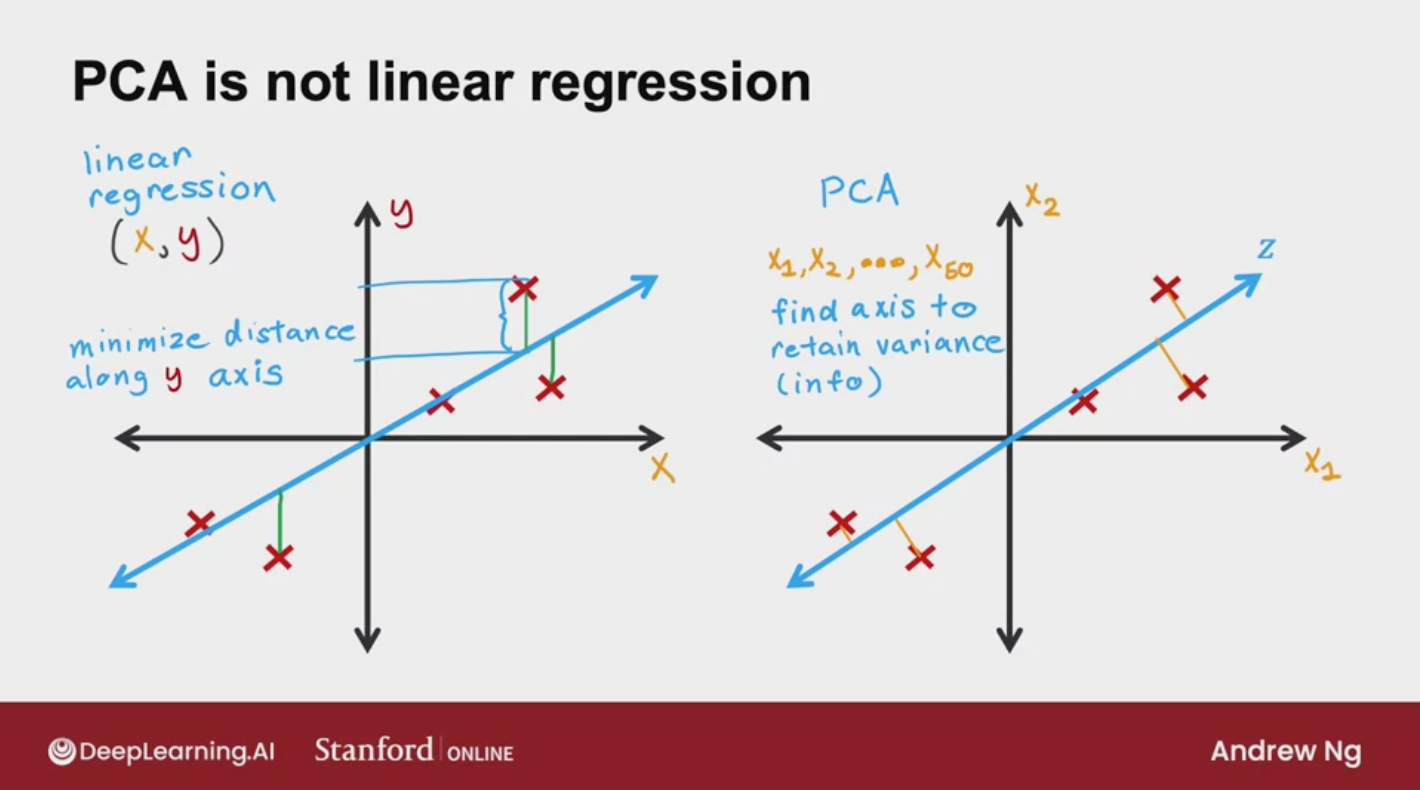
PCA is not linear regression
Approximation to the original data

PCA in code
Optional pre-processing: Perform feature scaling
- Fit the data to obtain 2 (or 3) new axes (principal components)
- Optionally examine how much variance is explained by each principal component
- Transform (project) the data onto the new axes


Applications of PCA
- Visualization: reduce to 2 or 3 features
- Less frequently used for
- Data compression (to reduce storage or transmission costs)
- Speeding up training of a supervised learning model